Abstract

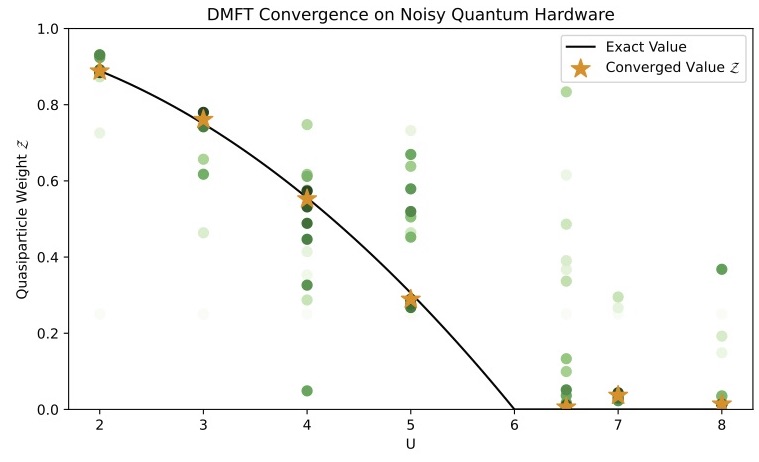
Dynamical mean-field theory (DMFT) maps the local Green’s function of the Hubbard model to that of the Anderson impurity model and thus gives an approximate solution of the Hubbard model from the solution of a simpler quantum impurity model. Accurate solutions to the Anderson impurity model nonetheless become intractable for large systems. Quantum and hybrid quantum-classical algorithms have been proposed to efficiently solve impurity models by preparing and evolving the ground state under the impurity Hamiltonian on a quantum computer that is assumed to have the scalability and accuracy far beyond the current state-of-the-art quantum hardware. As a proof of principle demonstration targeting the Anderson impurity model we, for the first time, close the DMFT loop with current noisy hardware. With a highly optimized fast-forwarding quantum circuit and a noise-resilient spectral analysis we observe both the metallic and Mott-insulating phases. Based on a Cartan decomposition, our algorithm gives a fixed depth, fast-forwarding, quantum circuit that can evolve the initial state over arbitrarily long times without time-discretization errors typical of other product decomposition formulas such as Trotter decomposition. By exploiting the structure of the fast-forwarding circuits we reduce the gate count (to 77 cnots after optimization), simulate the dynamics, and extract frequencies from the Anderson impurity model on noisy quantum hardware. We then demonstrate the Mott transition by mapping both phases of the metal-insulator phase diagram. Near the Mott phase transition, our method maintains accuracy where the Trotter error would otherwise dominate due to the long-time evolution required to resolve quasiparticle resonance frequency extremely close to zero. This work presents the first computation on both sides of the Mott phase transition using noisy digital quantum hardware, made viable by a highly optimized computation in terms of gate depth, simulation error, and runtime on quantum hardware. To inform future computations we analyze the accuracy of our method versus a noisy Trotter evolution in the time domain. Both algebraic circuit decompositions and error mitigation techniques adopted could be applied in an attempt to solve other correlated electronic phenomena beyond DMFT on noisy quantum computers.