Abstract

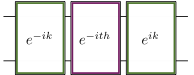
Simulating quantum dynamics on classical computers is challenging for large systems due to the significant memory requirements. Simulation on quantum computers is a promising alternative, but fully optimizing quantum circuits to minimize limited quantum resources remains an open problem. We tackle this problem by presenting a constructive algorithm, based on Cartan decomposition of the Lie algebra generated by the Hamiltonian, which generates quantum circuits with time-independent depth. We highlight our algorithm for special classes of models, including Anderson localization in one-dimensional transverse field XY model, where O(n^2)-gate circuits naturally emerge. Compared to product formulas with significantly larger gate counts, our algorithm drastically improves simulation precision. In addition to providing exact circuits for a broad set of spin and fermionic models, our algorithm provides broad analytic and numerical insight into optimal Hamiltonian simulations.