Abstract

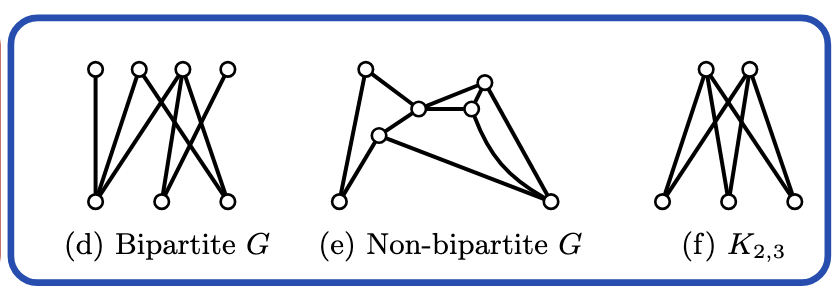
We provide a classification of all dynamical Lie algebras generated by 2-local spin interactions on undirected graphs. Building on our previous work where we provided such a classification for spin chains, here we consider the more general case of undirected graphs. As it turns out, the one-dimensional case is special; for any other graph, the dynamical Lie algebra solely depends on whether the graph is bipartite or not. An important consequence of this result is that the cases where the dynamical Lie algebra is polynomial in size are special and restricted to one dimension.