Abstract

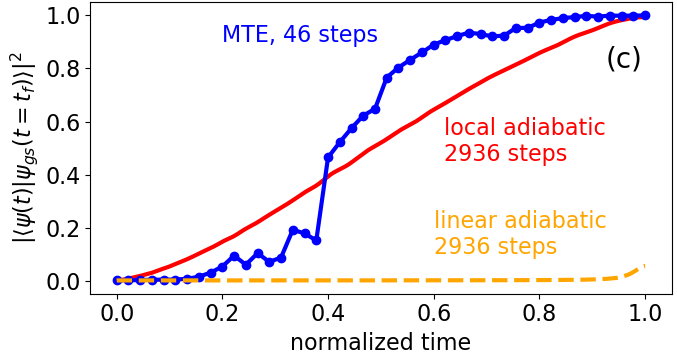
Adiabatic state preparation seeks to prepare the ground state of a target Hamiltonian from an easily prepared ground state of the initial Hamiltonian. It is guaranteed to work for time-dependent Hamiltonians that always have an energy gap to the first excited state throughout the entire evolution, but it can be excruciatingly slow. To speed up the process, we introduce a scaling factor that modulates the Hamiltonian during the time evolution, controlled by a variational principle on the final energy of the unscaled Hamiltonian. We find the optimized time evolution resembles a local adiabatic time evolution with an additional rapid modulation of the scale, which both reduces diabatic excitation from the ground state, and returns excited states back to the ground state. This approach is particularly simple to implement; it does not require constructing complicated counter-diabatic Hamiltonians nor does it need any a priori knowledge of the energy gap of the system. When the time evolution is discretized into problem and mixer components it closely resembles the quantum approximate optimization algorithm, featuring a local adiabatic field with oscillations arising from the ratio of angles at each layer and from a layer-dependent modulation of the overall scale.