Abstract

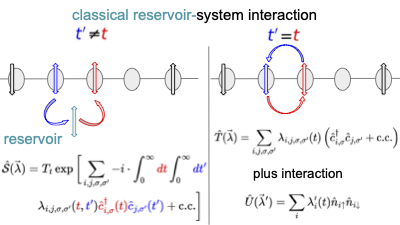
Preparing the ground state of the Fermi-Hubbard model is challenging, in part due to the exponentially large Hilbert space, which complicates efficiently finding a path from an initial state to the ground state using the variational principle. In this work, we propose an approach for ground state preparation of interacting models by involving a classical reservoir, simplified to the instantaneous-response limit, which can be described using a Hamiltonian formalism. The resulting time evolution operator consist of spin-adapted nearest-neighbor hopping and on-site interaction terms similar to those in the Hubbard model, without expanding the Hilbert space. We can engineer the coupling to rapidly drive the system from an initial product state to its interacting ground state by numerically minimizing the final state energy. This ansatz closely resembles the Hamiltonian variational ansatz, offering a fresh perspective on it.