Abstract

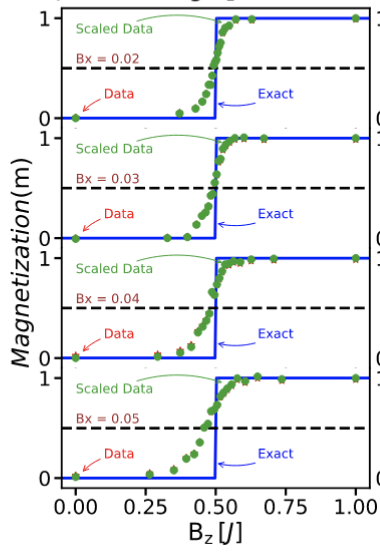
Quantum phase transitions materialize as level crossings in the ground-state energy when the parameters of the Hamiltonian are varied. The resulting ground-state phase diagrams are straightforward to determine by exact diagonalization on classical computers, but are challenging on quantum computers because of the accuracy needed and the near degeneracy of the competing states close to the level crossings. On the other hand, classical computers are limited to small system sizes, which quantum computers may help overcome. In this work, we use a local adiabatic ramp for state preparation to allow us to directly compute ground-state phase diagrams on a quantum computer via time evolution. This methodology is illustrated by examining the ground states of the XY model with a magnetic field in the z-direction in one dimension. We are able to calculate an accurate phase diagram on both two- and three-site systems using IBM quantum machines.