Abstract

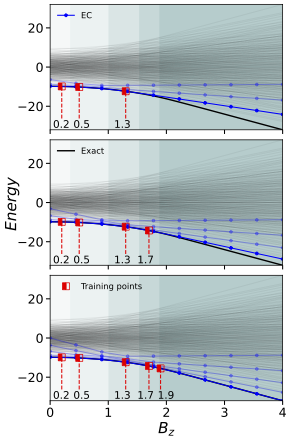
Quantum subspace diagonalization (QSD) methods are quantum-classical hybrid methods, commonly used to find ground and excited state energies by projecting the Hamiltonian to a smaller subspace. In applying these, the choice of subspace basis is critical from the perspectives of basis completeness and efficiency of implementation on quantum computers. In this work, we present Eigenvector Continuation (EC) as a QSD method, where low-energy states of the Hamiltonian at different points in parameter space are chosen as the subspace basis. This unique choice enables rapid evaluation of low-energy spectra, including ground and nearby excited states, with minimal hardware effort. As a particular advantage, EC is able to capture the spectrum across ground state crossovers corresponding to different symmetry sectors of the problem. We demonstrate this method for interacting spin models and molecules.