Abstract

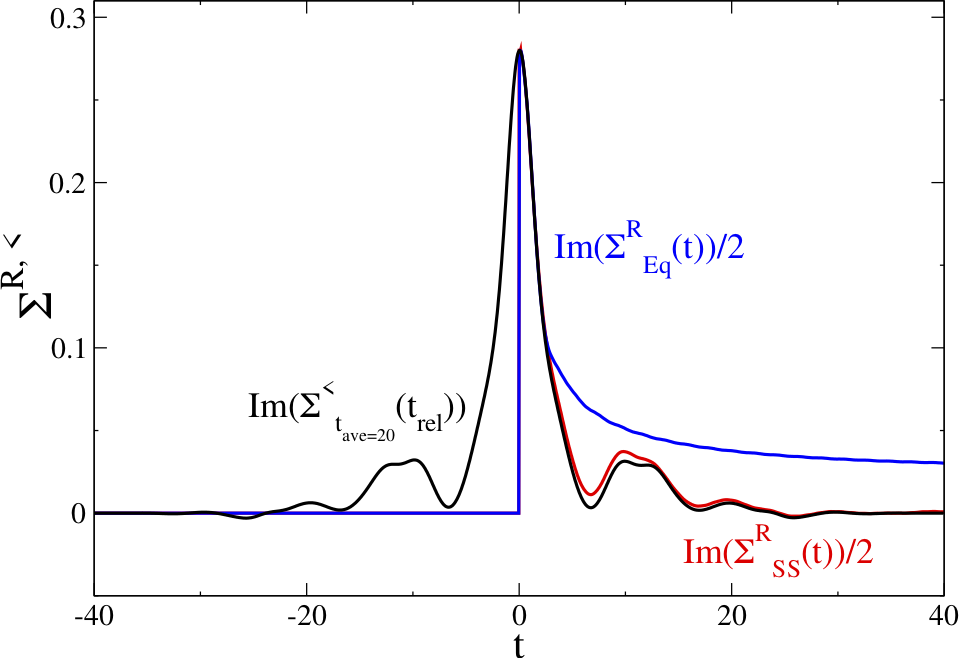
Many-body quantum systems in nonequilibrium remain one of the frontiers of many-body physics. While there has been significant advances in describing the short-time evolution of these systems using a variety of different numerical algorithms, it has been quite difficult to evolve a system from an equilibrium state prior to the application of a driving field, to the long-time steady (or periodically oscillating) state. These dynamics are complex: the retarded quantities tend to approach their long-time limit much faster than the lesser (or greater) quantities. Recent work on strongly correlated electrons in DC electric fields illustrated that the system may evolve through successive quasi-thermal states obeying an effective fluctuation-dissipation theorem in time. We demonstrate an extrapolation scheme that uses the short-time transient calculation to obtain the retarded quantities and to extract how the lesser/greater quantities vary with time and then extend the numerical solutions all the way to the steady state, with minimal additional computational cost. Our approach focuses on extrapolating the electronic self-energy and then employing that to determine the Green’s function and various experimentally relevant expectation values.