Abstract

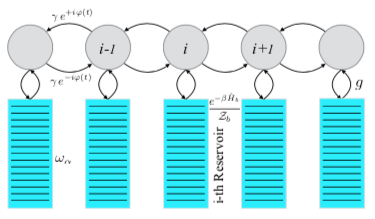
The driven-dissipative many-body problem remains one of the most challenging unsolved problems in quantum mechanics. The advent of quantum computers may provide a unique platform for efficiently simulating such driven-dissipative systems. But there are many choices for how one engineers the reservoir. One can simply employ ancilla qubits to act as a reservoir and then digitally simulate them via algorithmic cooling. A more attractive approach, which allows one to simulate an infinite reservoir, is to integrate out the bath degrees of freedom and describe the driven-dissipative system via a master equation. But how accurate is this for a fermionic bath? In this work, we use the exact solution for a noninteracting driven-dissipative system to benchmark the accuracy of this master-equation formalism. Such a master equation can be directly implemented on a quantumcomputer. The Kraus map required to do this enables us to create a quantum circuit that reproduces the dissipative dynamics. Because partial resets are not available in current quantum hardware, we simulate only the simplest example of such a Kraus map on an IBM machine, which can be simulated exactly without requiring any resets. The simulations are in excellent agreement with the exact results.